Возведение в степень (100 статья на портале) - Математика

Возведение в степень (100 статья на портале)

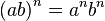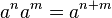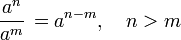$\left(ab\right)^n = a^nb^n$ $\left({a\over b}\right)^n = {{a^n}\over{b^n}}$ $a^na^m = a^{n+m}\!$ $\left. {a^n\over {a^m}} \right. = a^{n-m},\quad n > m$ $\left(a^n\right)^m = a^{nm}$ запись $a^{n^m}$ не обладает свойством ассоциативности (сочетательности), то есть в общем случае левая ассоциативность не равна правой ассоциативности $(a^n)^m \ne a^\left({n^m}\right)$ , результат будет зависеть от последовательности действий, например, $(2^2)^3=4^3=64\!$ , а $2^\left({2^3}\right)=2^8=256$ . Принято считать запись $a^{n^m}$ равнозначной $a^\left({n^m}\right)$ , а вместо $(a^n)^m$ можно писать просто $a^{nm}$ , пользуясь предыдущим свойством. возведение в степень не обладает свойством коммутативности (переместительности): вообще говоря, $a^b\ne b^a$ , например, $2^5=32$ , но $5^2=25$ . Источник: http://ru.wikipedia.org/wiki/%C2%EE%E7%E2%E5%E4%E5%ED%E8%E5_%E2_%F1%F2%E5%EF%E5%ED%FC
1 2 3 4 5 Категория: Математика \| Добавил: teacher (06.08.2012)
Просмотров: 981 \| Рейтинг: 5.0/1